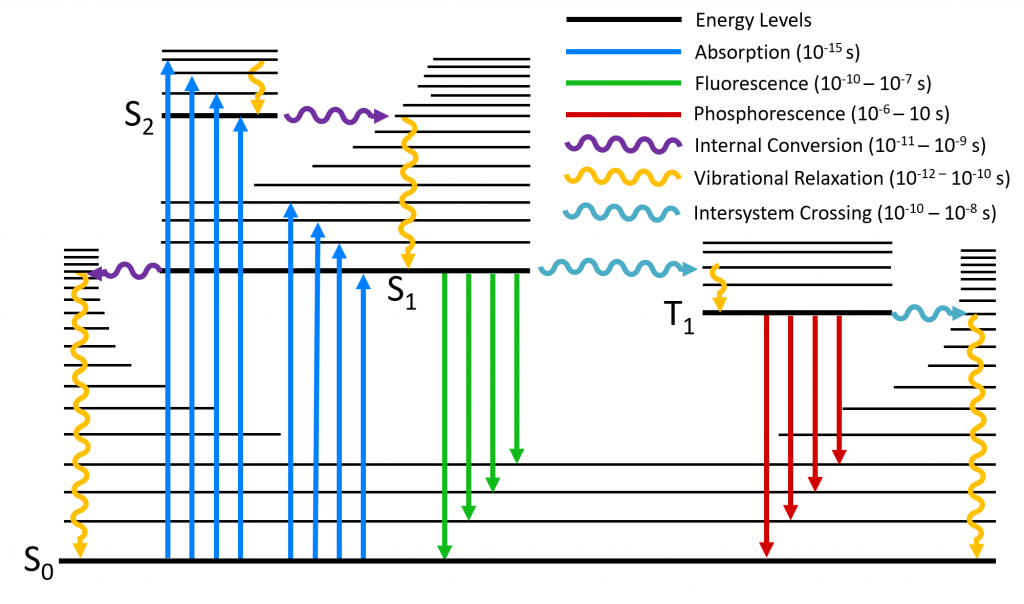
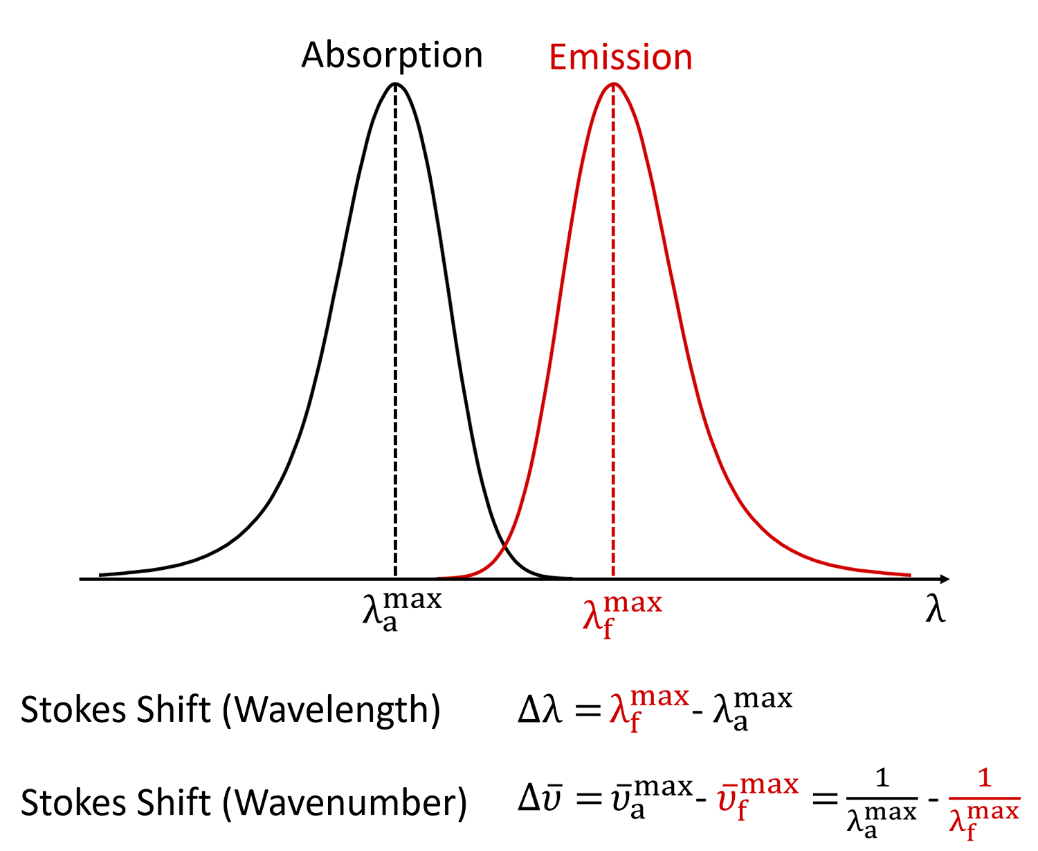
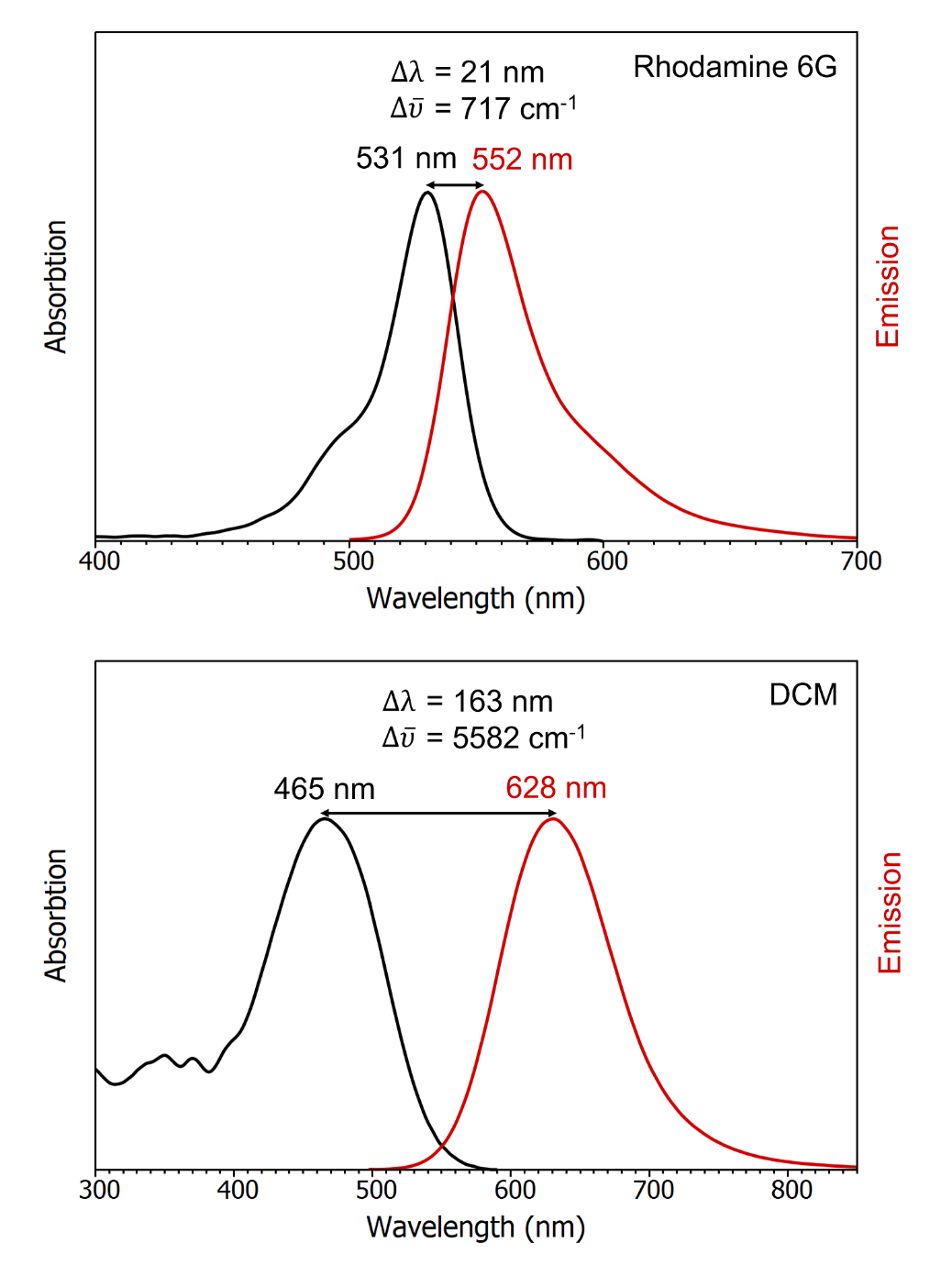
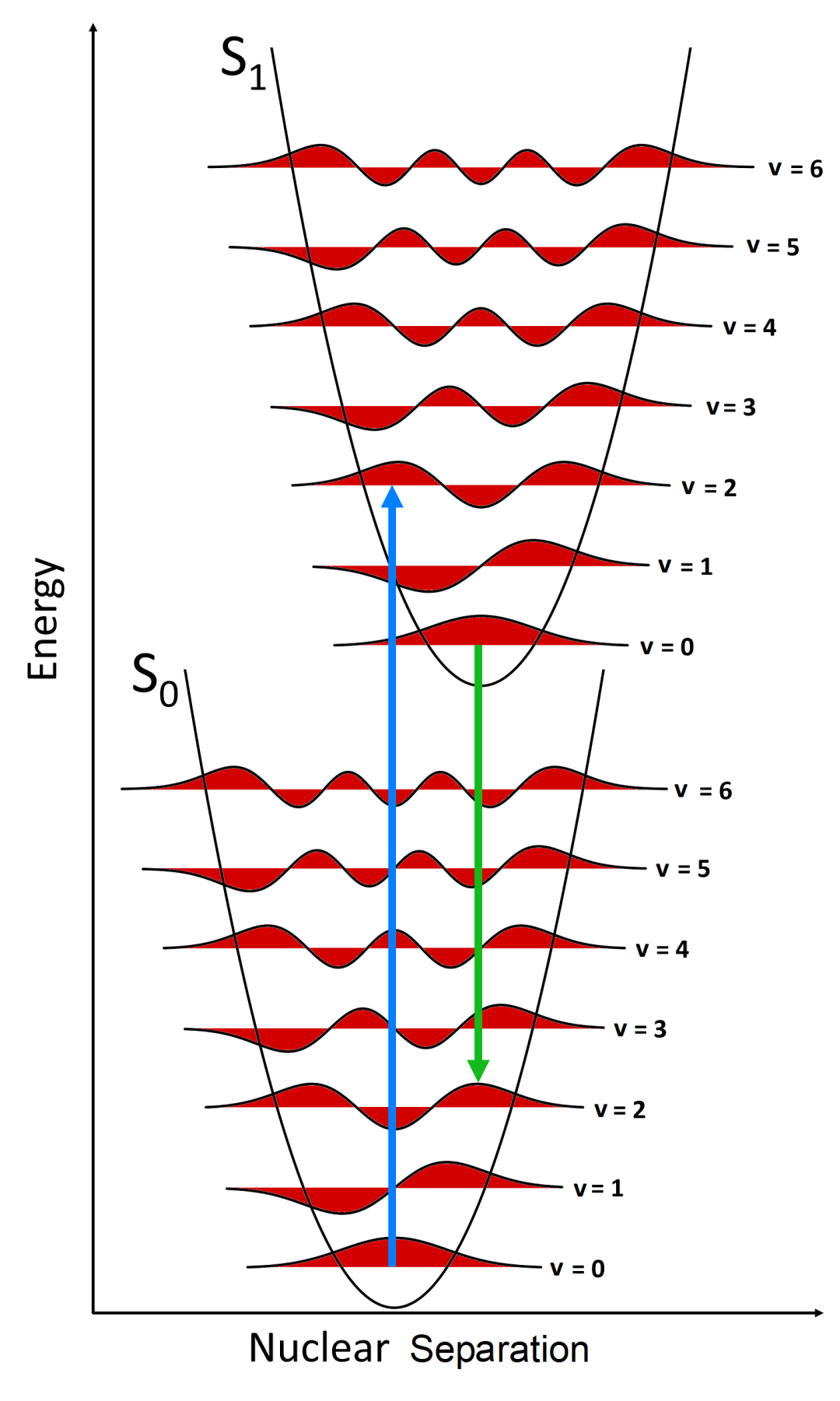
Jablonski能级图清楚地可视化了分子在受到光激发后可能产生的跃迁情况。

吸收能量（Absorption）：如图中蓝色箭头所示，分子通过吸收光子从基态跃迁到更高能级，这是雅布隆斯基能级图中最快的跃迁过程，发生在10⁻¹⁵秒量级的时间尺度上。室温条件下，根据玻尔兹曼分布，体系中大多数分子都处于基态的最低振动能级，因此图中显示的吸收过程均起始于该能级。分子吸收光子后，会从基态S₀跃迁至单重激发态（S₁、S₂等）的某个振动能级；此外由于角动量守恒的限制，分子不能直接被激发至三重激发态（T₁、T₂等）。

振动弛豫（Vibrational Relaxation）：分子吸收能量跃迁至激发态后，处于不稳定状态，最终会通过能级弛豫过程返回到基态。首个能量耗散途径是振动弛豫（橙色箭头）：过剩的振动能量通过分子内或分子间振动传递，直至达到电子态的最低振动能级。振动弛豫过程极其迅速，发生在10⁻¹² - 10⁻¹⁰ s的时间尺度上，其速率快于其他所有跃迁过程。

内转换（Internal Conversion）：处于较高单重激发态的分子也可能通过内转换过程（紫色箭头）向较低的单重激发态跃迁。内转换过程发生后会立即伴随振动弛豫，使分子跃迁至该电子态的最低振动能级。内转换的速率与两电子态之间的能隙成反比；对于能级间隔较小的高能级单重激发态（如S₃→S₂、S₂→S₁等），其内转换过程极其迅速，发生在10⁻¹¹ - 10⁻⁹ s内。而S₁与S₀态之间的能隙要大得多，这两个电子态之间的内转换过程耗时更长，并且会与荧光、系间窜越等其他跃迁过程形成竞争。

荧光（Fluorescence）：荧光产生于S₁→S₀的跃迁过程中（绿色箭头，10⁻¹⁰ - 10⁻⁷ s），由上述的振动弛豫和内转换的快速进行，且Kasha规则[1]指出对于多重态的分子，光子仅能由最低激发态发射；因此除少数情况外，荧光发射均产生于分子从第一电子激发态S₁的最低振动能级跃迁回单重态基态S₀的这一过程。此现象也导致了斯托克斯位移（Stokes-Shift）的产生，即荧光发射波长大于激发波长。

系间窜越（Intersystem Crossing）：作为荧光和内转换之外的一种弛豫途径，允许分子从第一激发单重态S₁跃迁至第一激发三重态T₁。因自旋角动量守恒，该跃迁本属禁阻过程；然而，借助自旋角动量与轨道角动量间的耦合效应（即自旋-轨道耦合），该过程可转变为弱允许跃迁。系间窜越与S₁态内转换和荧光过程存在竞争关系，所以对于大多数纯有机分子而言，此过程速率过慢而不具显著意义。提升系间窜越速率的一种有效策略是在分子中引入重原子，通过增强自旋-轨道耦合强度来实现。完成系间窜越后，分子会立即通过振动弛豫降至T₁态的基振动能级。

磷光（Phosphorescence）：磷光来自于T₁→S₀跃迁发射光子的过程。与系间窜越相似，磷光在理论上属于禁阻跃迁，但通过自旋-轨道耦合作用可弱允许发生。这种跃迁的禁阻特性导致磷光衰退速率常数极低，因此其发生的时间尺度远大于荧光，典型的磷光寿命范围在10⁻⁶ - 10 s。

延迟荧光（Delayed Fluorescence）：第三种辐射跃迁类型被称为延迟荧光，延迟发光的产生源于处于T₁态的分子先跃迁至S₁态，继而通过辐射跃迁返回S₀态；这导致此过程发射的光波长与标准荧光完全相同，但发生在更长的时间尺度上。

参考来源